Unitary Representations via the Orbit Method

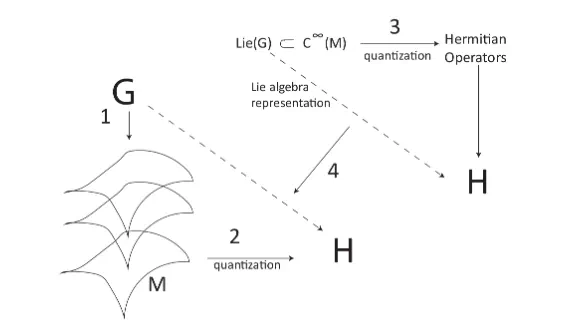
The orbit method, developed by A.A. Kirillov, bridges representation theory and symplectic geometry, offering a geometric framework for constructing unitary representations of Lie groups. This paper explores the method’s foundational concepts, focusing on coadjoint orbits as symplectic manifolds and their quantization via geometric quantization techniques. Unitary representations of specific groups, including SU(2) and the Heisenberg group, are derived, demonstrating the method’s efficacy in linking geometric structures with harmonic analysis. Applications to various classes of Lie groups are discussed, highlighting the method’s versatility and limitations. The orbit method emerges as both a conceptual and computational tool, offering insights into representation theory and quantum mechanics through a unified mathematical lens.