Improved Hamiltonian Learning with Neural Differential Equations using Classical Shadows

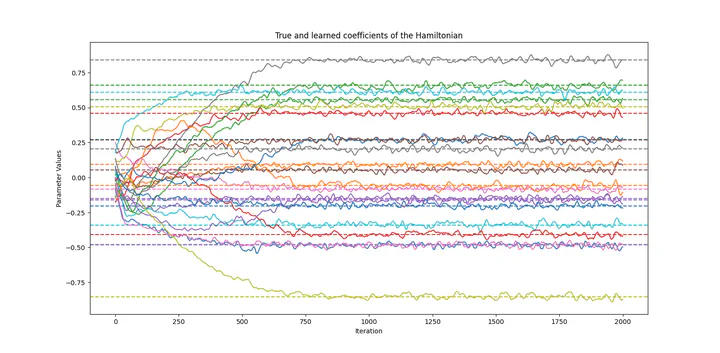
The Hamiltonian Learning (HL) problem consists of the task of inferring the Hamiltonian of a many-body system given a set of state trajectories of that system. The problem is highly relevant for error mitigation, optimal quantum control, quantum simulation, and device certification. In [T. Heightmann et al., 2024] introduced a novel approach to solving the HL problem on quantum many-body spin systems using neural differential equations (NODEs). Their proposed method combines an Ansatz Hamiltonian with NODEs to infer the quantum dynamics of a many-body system. The authors showcased the reliability and expressiveness of their method by solving several previously unsolved HL problems in one-dimensional spin-1/2 chains. However, the loss function used to train the parameters $\theta$ for both the Ansatz Hamiltonian and the neural network is calculated as the average negative log-likelihood of the probabilities $|\langle b|\psi_{\theta}(t)\rangle |^2$ using Born’s rule for the bitstrings b in a subset of the given dataset corresponding to all bitstrings measured at the same timestamp and input state as the estimator $\psi_{\theta}(t)$. Despite several other challenges, the authors highlight that such a loss function relies on an accurate estimate of the log-likelihood of a small number of Pauli strings. This could bias the loss function if the number of measurement bases is insufficient or measurements are noisy. At the same time, the authors note the possibility of using classical shadows introduced in [H. Huang, R. Kueng, and J. Preskill, 2020] to eliminate these disadvantages. In this project, we will elaborate on this idea by modifying the loss function by tracking expectation values in time using classical shadows. We will do this by generating classical shadows for the evolved states $|\psi_{\theta}(t)\rangle$ and calculating a new loss function on that basis. We expect the method in [T. Heightmann et al., 2024] using our new loss function to have numerous advantages over using the old one. In particular, we expect that the two challenges mentioned in [T. Heightmann et al., 2024] can be resolved. The limited coverage of Pauli bases can be overcome using classical shadows, which enable more accurate reconstruction of the probabilities $|\langle b|\psi_{\theta}(t)\rangle|^2$ by aggregating data across different random measurement bases, while their randomized nature ensures uniform Hilbert space sampling and mitigates biases from restricted measurement bases. Second, classical shadow protocols are designed to be robust against certain types of noise [D. Koh and S. Grewal, 2022]. To explore the benefits of the new loss function, we aim to implement the algorithm with our modified loss function and benchmark it against the algorithm using the old loss function from [T. Heightmann et al., 2024].